Logistic Regression
도입
Logistic Regression은 분류를 목적으로 한다. 즉, 주어진 입력에 따라 discrete한 클래스를 추정한다.
Binary Classification
(0 or 1, False or True)
이를 위해서 기준이 되는 임계 함수를 두는데, 이 함수는 계단 모양이라서 0 아니면 1인 값을 가지게 된다.
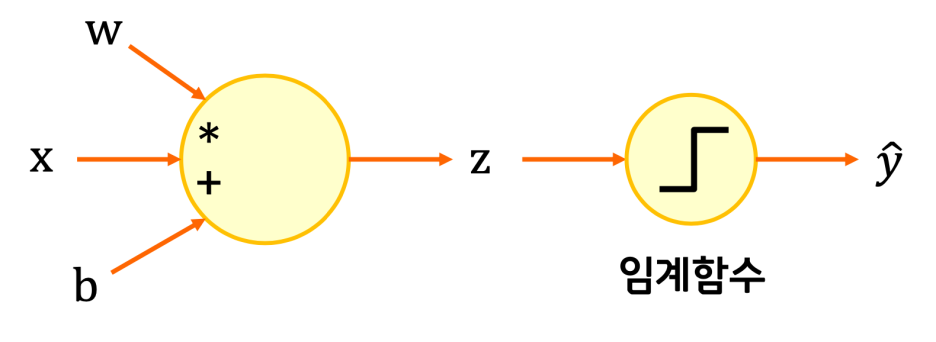
다만 이전의 Linear regression 모델에서 바로 임계함수를 적용하면 아래와 같은 문제가 발생할 수 있다.
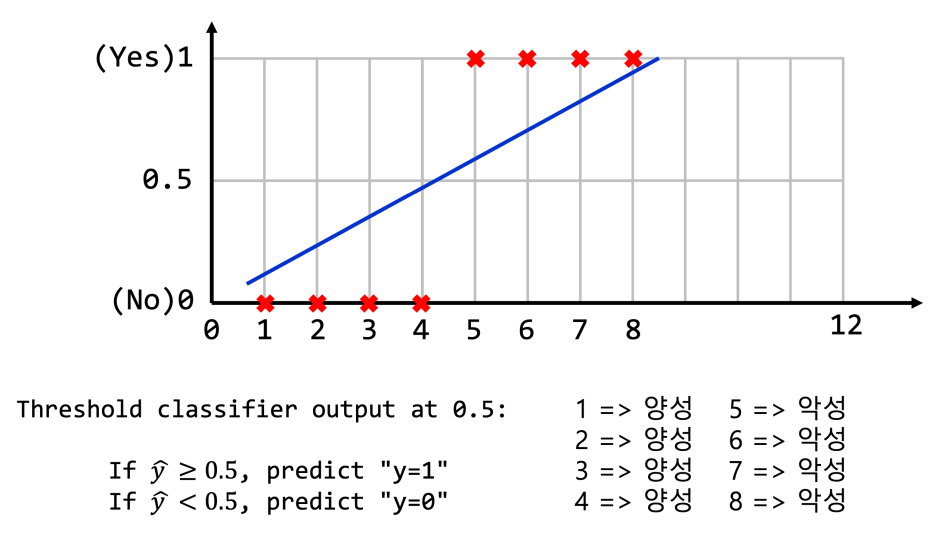
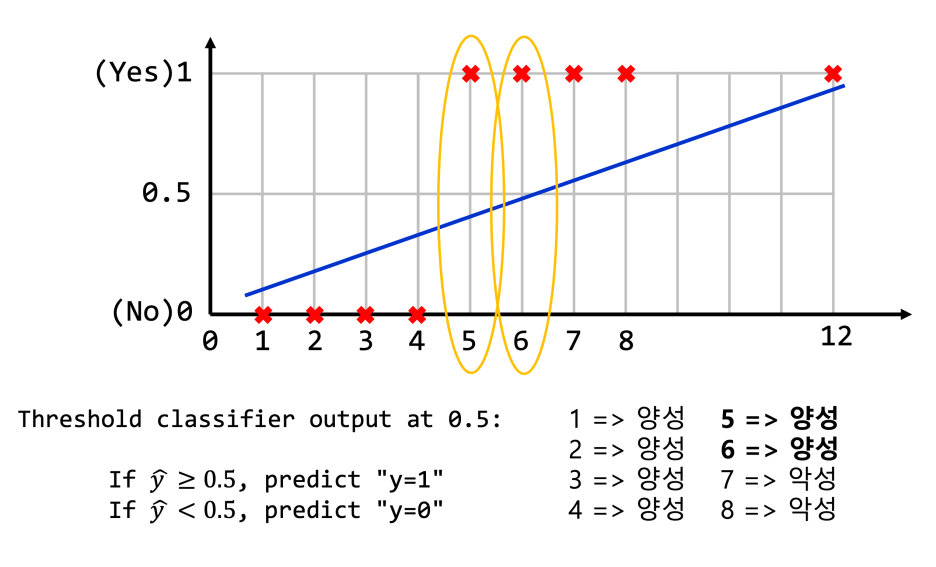
0.5를 기준으로 악성인 5, 6번이 새로운 데이터에 의해 양성으로 바껴버릴 수 있다.
직선을 기반으로는 나누기가 어려운 것이다.
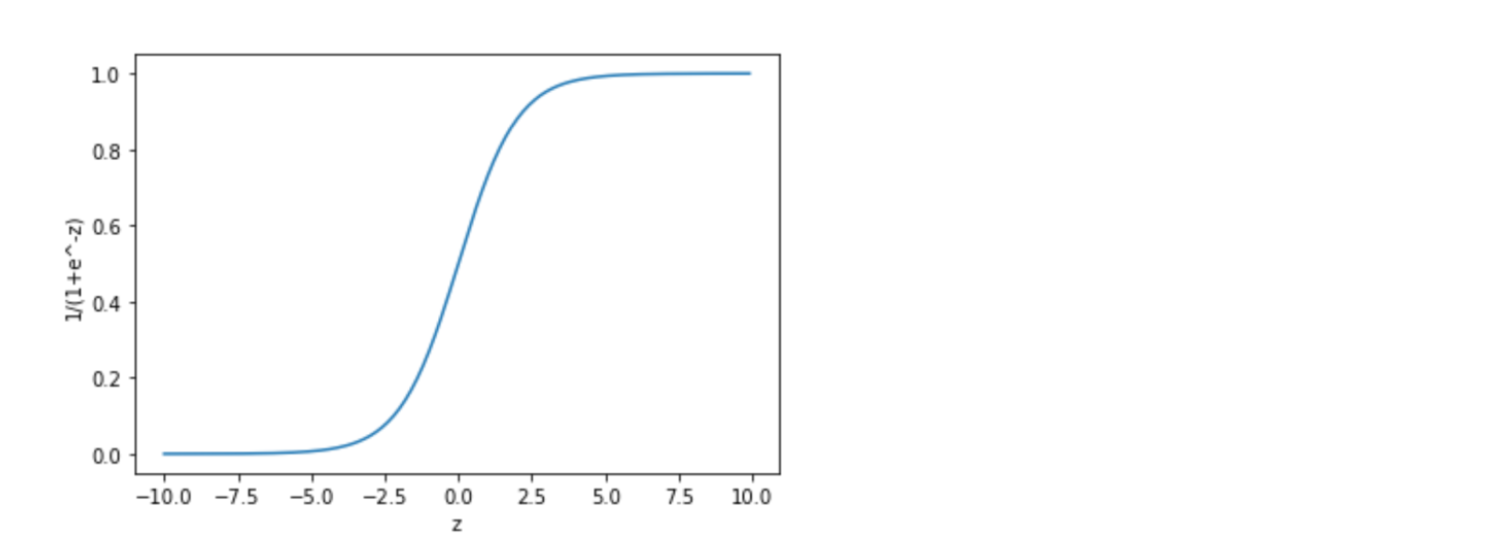
Sigmoid 함수
그래서 우리는 중간에 활성화 함수 단계를 두어서 이를 해결한다.
Sigmoid 함수…스타트업 드라마에서도 남주혁이 쓰더라.

이렇게 생긴 함수이며 아래와 같은 수식으로 표현한다.
1 / (1 + e^-x)
여기서 학습할 변수를 추가하면,
1/(1 + e^-(WX+b))
이렇게 될 것이다.
이 경우 Linear Regression처럼 아름다운 Convex 형태(극점이 유일)가 아니기 때문에 (이전에는 그냥 2차함수의 그래프였을 뿐이므로), Cost function에 Gradient Descent방식을 사용하기가 어렵다.
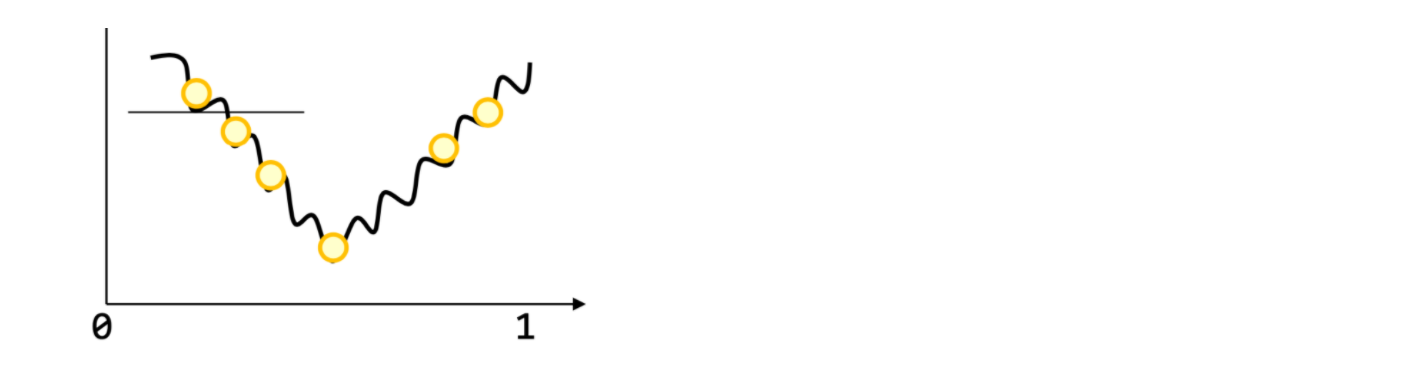
Binary Cross Entropy Error 방식
그래서 우리는 Binary Cross Entropy Error 방식을 사용한다. 엔트로피란다…점점 어려운 느낌이 들지만…여차저차해서 계산이 끝나면 쉬운 포맷이 나오더라. 참자. 그래서 결과적으로 아래와 같은 형태의 비용함수가 나오게 되는 것이고,
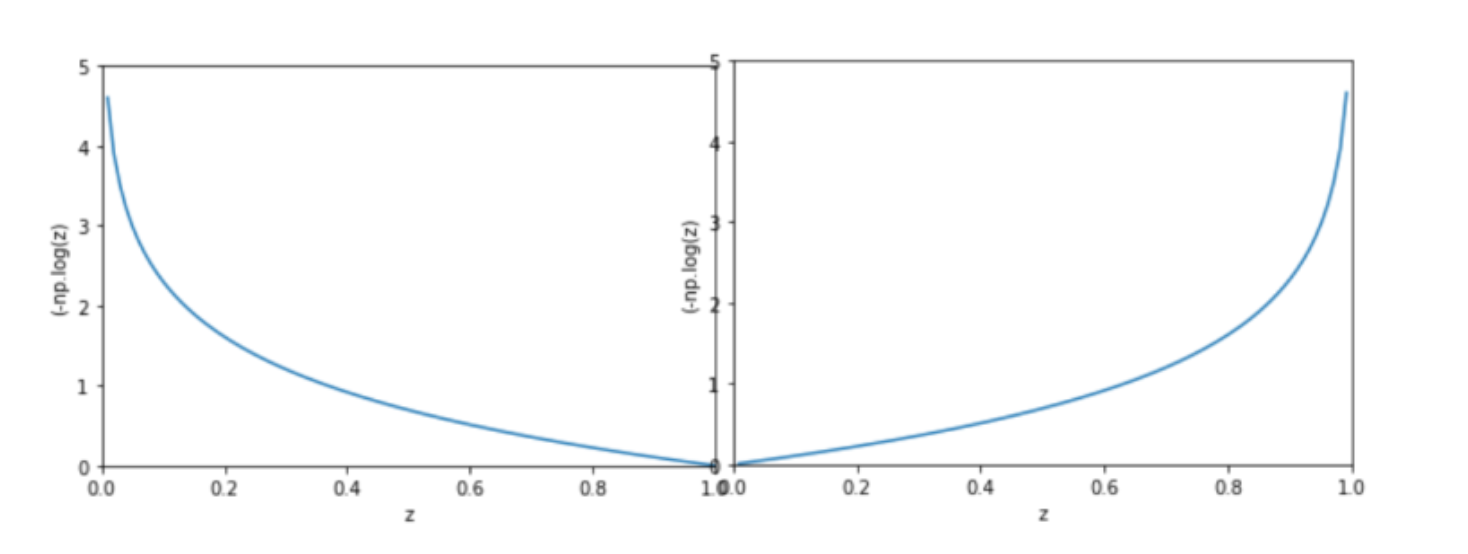
실제 정답(label)의 확률 분포와 h(x)의 확률분포를 cost로 계산하면, cost가 0에서 무한대까지의 형태로 표현이 가능하고 위와 같이 극점이 하나인 형태로 나타낼 수 있는 것이다. 즉, 여기서부터는 로그함수의 형태라서 이전처럼 Gradient Descent를 이용할 수 있다.
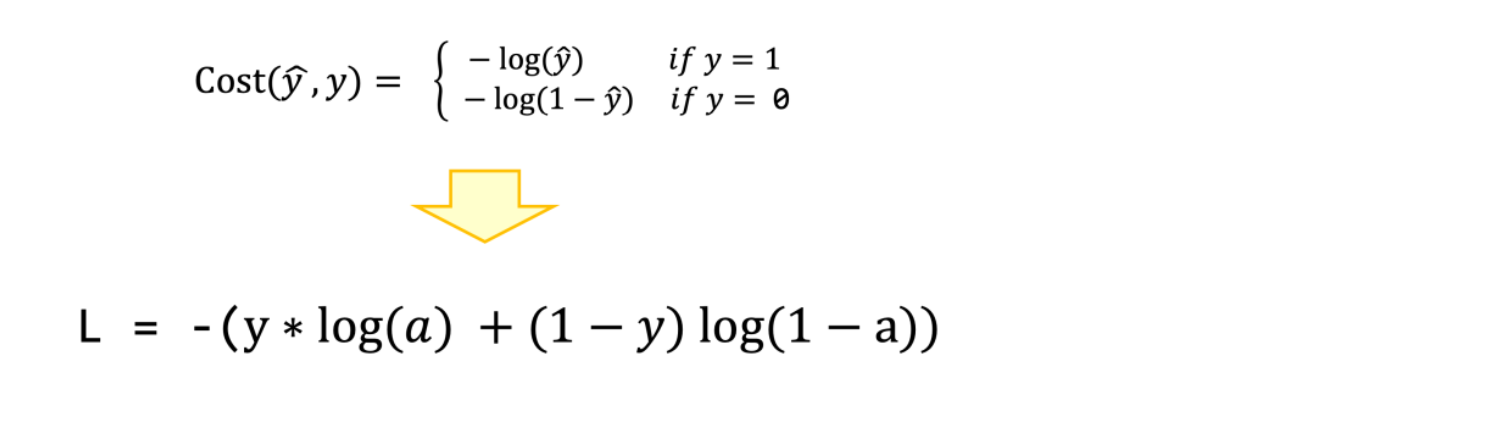
수식으로 표현하면 cost function은 위와 같다. 이제 cost에 대해서 미분을 해서 역전파를 해야하는데 이런 저런 계산을 거치고 나면,
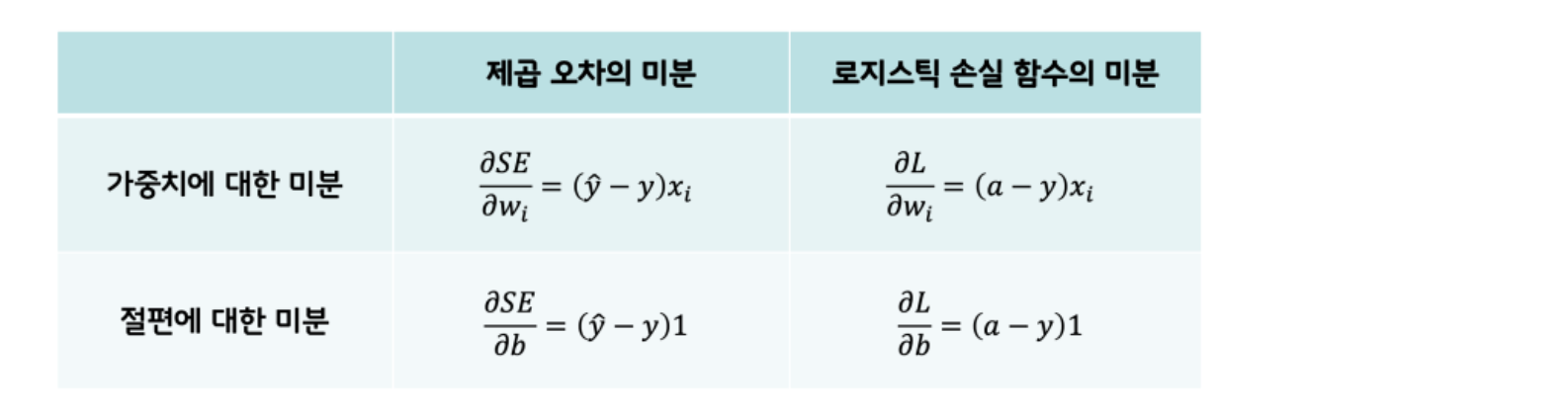
기존 y_hat 부분이 a(sigmoid 함수의 결과값)로 바뀌었을 뿐 계산법은 같다.
구현 코드
import matplotlib.pyplot as plt
import numpy as np
class Neuron:
def __init__(self):
self.w = 1.0 # 가중치를 초기화합니다
self.b = 1.0 # 절편을 초기화합니다
def forpass(self, x):
z = x * self.w + self.b # 직선 방정식을 계산합니다
return z
def backprop(self, x, err):
w_grad = x * err # 가중치에 대한 그래디언트를 계산합니다
b_grad = 1 * err # 절편에 대한 그래디언트를 계산합니다
return w_grad, b_grad
def activation(self, z):
a = z;
a = 1/(1+np.exp(-z))
return a
def fit(self, x, y, epochs=200):
for i in range(epochs): # 에포크만큼 반복합니다
for x_i, y_i in zip(x, y): # 모든 샘플에 대해 반복합니다
z = self.forpass(x_i) # 정방향 계산
a = self.activation(z)
err = a - y_i # 오차 계산
w_grad, b_grad = self.backprop(x_i, err) # 역방향 계산
self.w -= 0.1*w_grad # 가중치 업데이트
self.b -= 0.1*b_grad # 절편 업데이트
# x = np.array([1,2,3,4,5,6,7,8])
# y = np.array([0,0,0,0,1,1,1,1])
x = np.array([1,2,3,4,5,6,7,8,20])
y = np.array([0,0,0,0,1,1,1,1,1])
neuron = Neuron()
neuron.fit(x, y)
for xi, yi in zip(x,y):
plt.plot(xi,yi,"rx")
for x_i in x:
y_hat = neuron.forpass(x_i)
a = neuron.activation(y_hat)
if( a >= 0.5 ):
print("%d : 악성종양"%x_i)
else:
print("%d : 양성종양"%x_i)
y_temp.append(a)
x = np.arange(0,x[-1],0.1)
y_temp = []
for i, x_i in enumerate(x):
y_hat = neuron.forpass(x_i)
a = neuron.activation(y_hat)
y_temp.append(a)
plt.plot(x,y_temp)
plt.show()
구현 코드도 크게 다르지 않다. forpass 결과값에 대해서 sigmoid(activation) 함수를 돌려서 a값을 얻어내고 이것을 이용하는 형태이다.
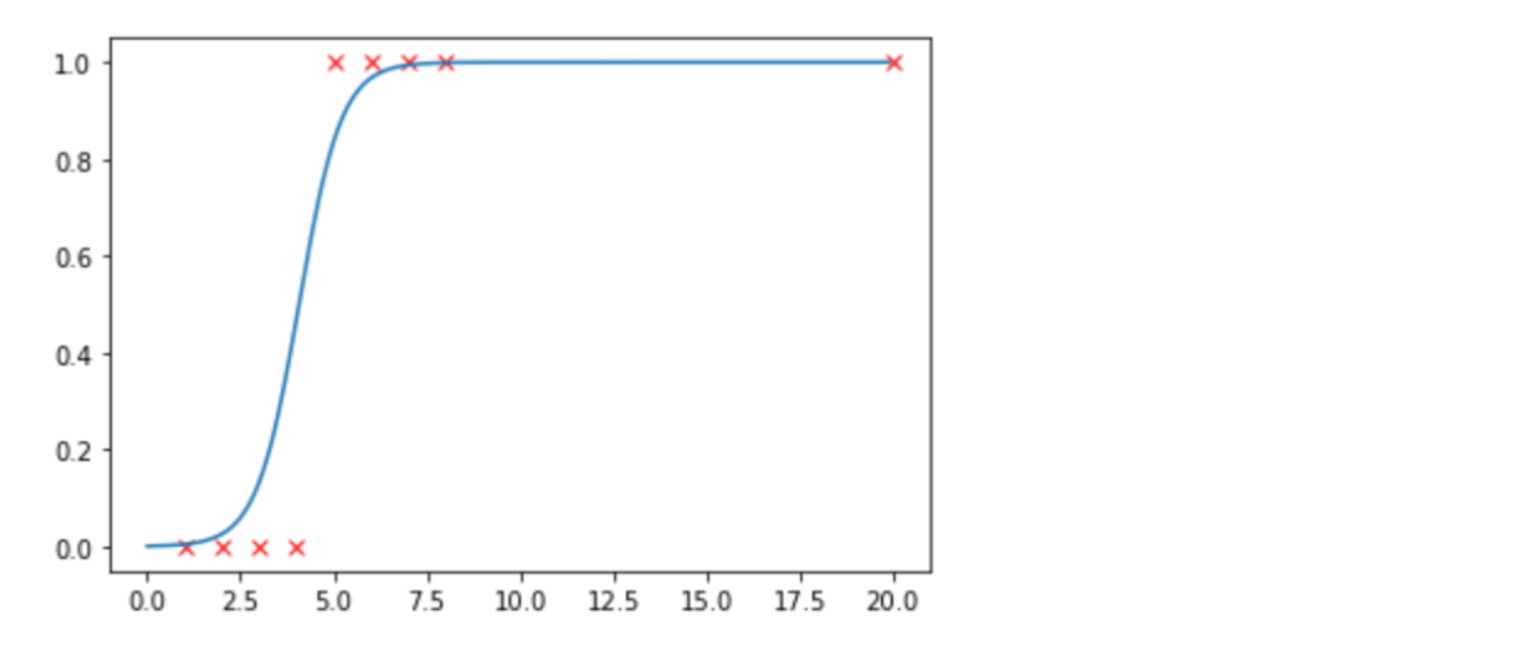
이렇게 했더니 새로운 데이터에도 끄떡없게 된다.
결과적으로는 구현과 수식에 있어서 크게 다른게 없었다.
이제 저기서 절반을 나눠서 양성, 음성 등으로 구분을 하면 될 것이다.