선형 회귀(Linear Regression)
도입
- 선형회귀란 평균으로 돌아간다는 의미이다.
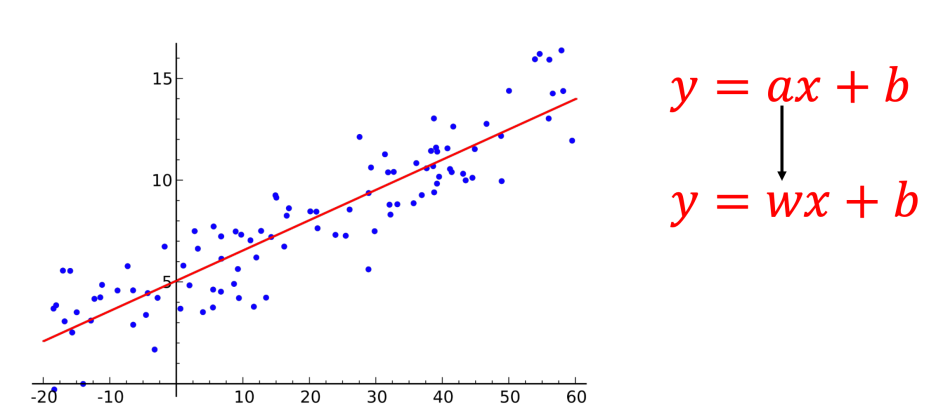
머신러닝의 기본 프로세스
Hypothesis(가설) 설정: 데이터의 분포를 보고 모델을 선택Cost Function 설정: 모델을 기반으로 랜덤값을 넣었을때, 정답과의 차이(Label이 있어야함)를 평가하는 로직.Learning algorithm 설계: Cost Function의 결과를 바탕으로 변수를 수정하며 정답을 찾아나가는 과정
위 기본 프로세스에 의하면,
Hypothesis(가설) 설정
우선 시각화된 데이터의 분포를 보니 1차 함수인거 같다. 모델을 수립한다.
H(x) = wx + b
H(x)는 ^y(y hat)로 표기하기도 하며 가설을 의미한다. 그리고 w(weight)는 기울기, b(bias)는 y절편을 의미한다.
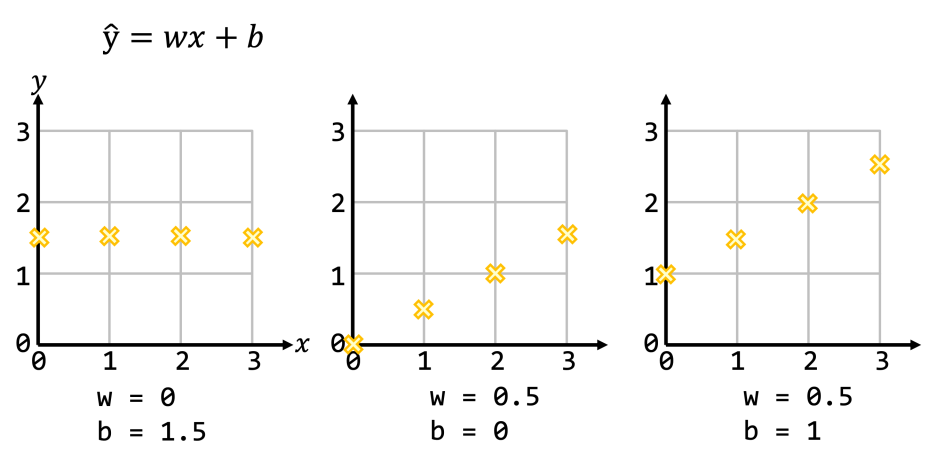
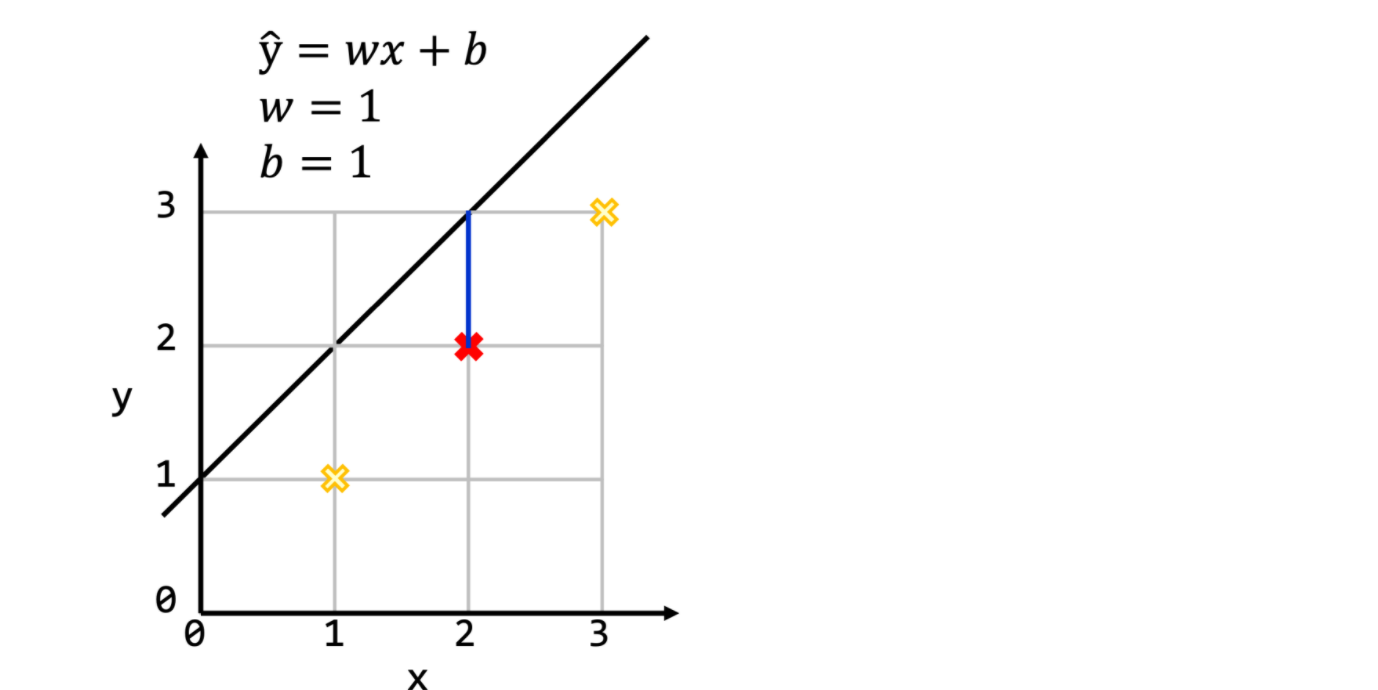
아래 코드는 y = x라는 직선에 대해서 weight와 bias를 1로 잡았을때,
실제값과 계산값의 차이를 그래프로 보여준다.
import numpy as np
import matplotlib.pyplot as plt
x = np.array([1,2,3])
y = np.array([1,2,3])
w = 1
b = 1
y_hat = np.zeros(3)
for i in range(len(x)):
y_hat[i] = w * x[i] + b
plt.plot(x, y, ‘o’)
plt.plt(x, y, ‘r-)
plt.plot(x, y_hat, ‘o’)
plt.plt(x, y_hat, ‘b-) # 삘간 선
plt.grid(True)
plt.show()
Cost Function 설정
- 편차를 그냥 내면 음양의 합 등으로 정확하지 않을 수 있다. 그래서
Mean Squared Error방식을 사용한다. - 정답(y)과 결과(H(x))의 차(Error)의 제곱의 평균을 내는 방식으로 큰 편차는 더 커져서 도드라진다. 이것이 제곱을 하는 이유이며 오차를 보기 쉬워진다.
Cost function = (시그마(H(x) - y)^2)
weight와 bias가 한개의 쌍만 있을때는,
J(w,b) = (1 / 2) * (H(x) - y)^2
가 된다.
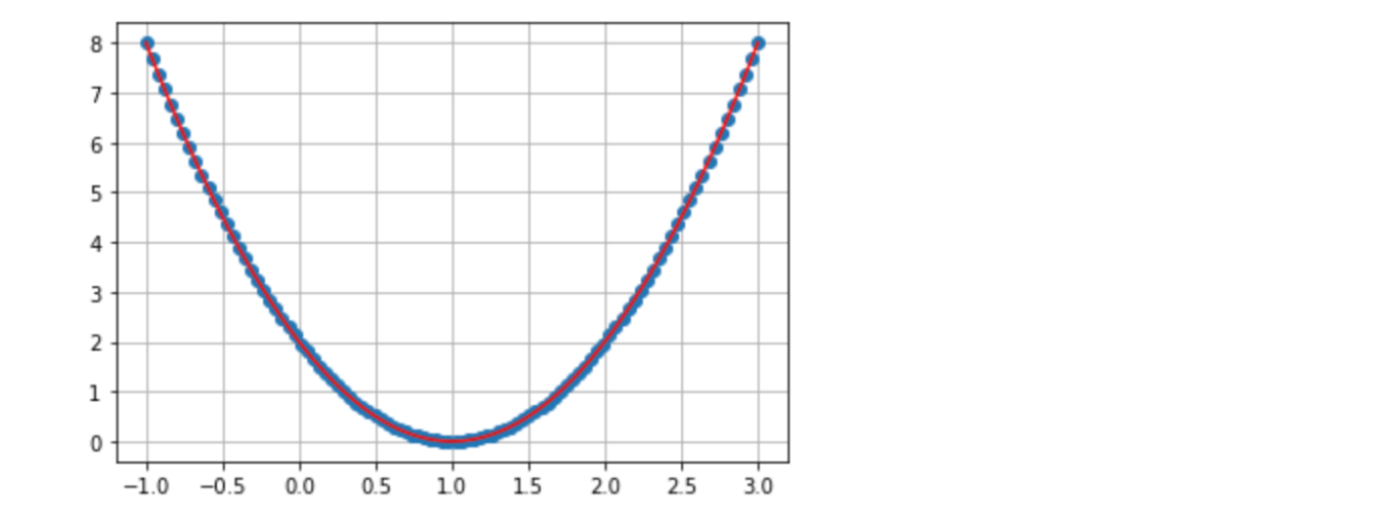
위에서 구한 함수는 2차 함수가 된다. 학습이란 Cost가 최소가 되도록 Hypothesis의 파라메터를 조절하는 것이다. (Weight와 Bias를 조절) 아래는 weight를 조절해서 cost가 제일 적은 w를 찾는 코드이다. 그래프에서 보듯 1일때 비용이 최소이다.
import numpy as np
import matplotlib.pyplot as plt
w = np.linspace(-1, 3, 100)
b = 0
j = np.zeros(100)
for i in range(len(w)):
y_hat = w[i] * 2 + b
j[i] = 0.5 * (y_hat - 2) ** 2
plt.plot(w, j, ‘o’)
plt.plt(w, j, ‘r-)
plt.grid(True)
plt.show()
제곱을 사용해서 물론 이차함수의 형태를 나타낸다.
Learning algorithm 설계
Stochastic Gradient Descent(SGD)
어느 방향으로 값을 조절할지를 알아내기 위해 접선의 기울기를 이용한다. 이는 많은 최소화 문제에 사용되고 끝까지 비슷한 방식을 사용한다. (접선의 기울기가 양이면 점점 편차가 늘어나고 있는것이므로 왼쪽으로, 반대면 오른쪽으로 진행한다)
weight -= LearningRate * 접선의 기울기
작동방식은 아래와 같다.
- 초기 추측으로 시작
- 0,0 (또는 다른 값)에서 시작
- W와 b를 약간 변경하여 cost(W, b)의 비용을 줄이려고 노력
- 매개 변수를 변경할 때마다 가능한 가장 낮은 cost(W, b)을 감소시키는 기울기를 선택
- 반복
- 최소한의 지역으로 수렴 할 때까지 수행
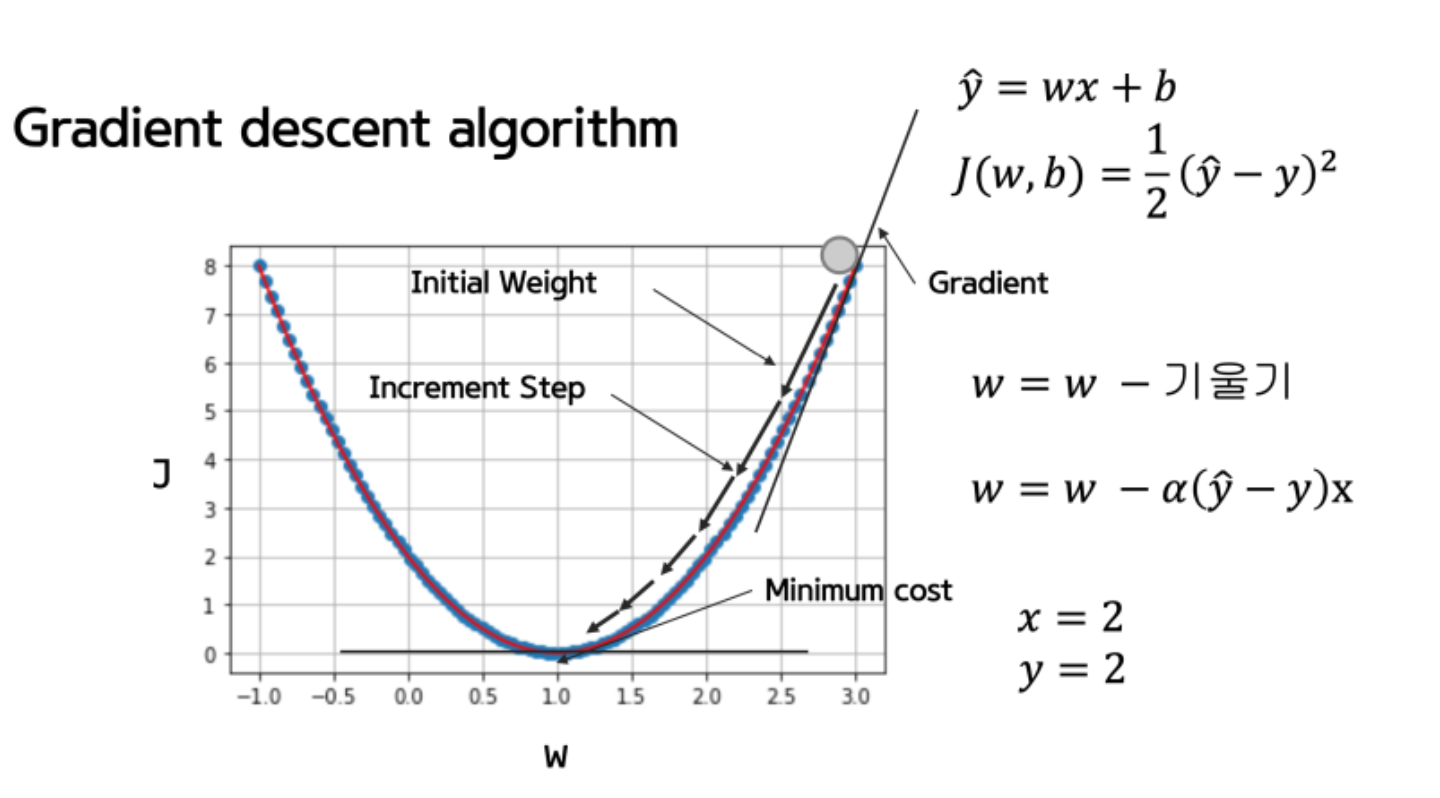
Learning Rate는 진행의 속도이며, 접선의 기울기가 크면 크게 접선의 기울기가 작으면 적게 조절하는 것도 좋다. (기울기가 작다는것은 정답에 근접했다는 뜻이며 문자로는 뮤로 표기한다) 그러나 값이 너무 크면 발산해서 영원히 정답이 안나올수있다. 처음에는 매우 작은 소수점값으로 해본다. 다만 이 경우 탐색양이 더 많아져 오래걸린다. 경험의 영역이라 할 수 있다. W, b는 machine이 구하지만 뮤는 사용자의 선택이다.
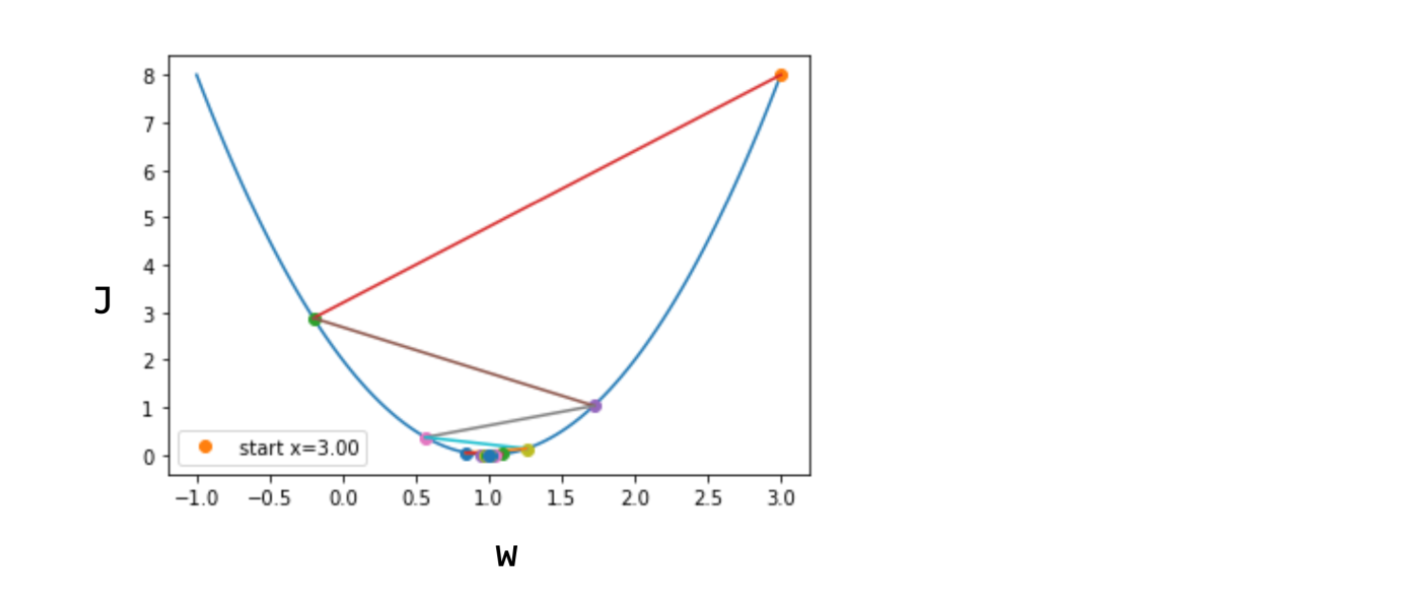
Learning Rate가 커서 아름답지 못하게(?) 답을 찾아가고 있다
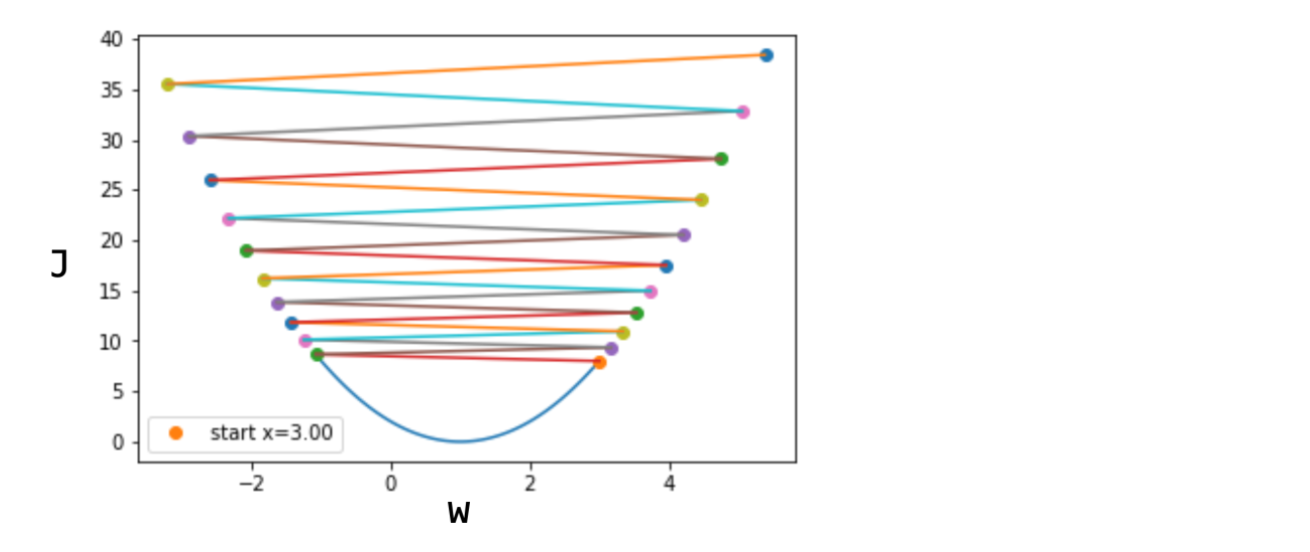
이번엔 답을 찾아가기는 커녕 발산하고 있다
이와 같이 접선의 기울기로 극저점을 찾아 정답을 찾는 방식을 Gradient Descent Algorithm(경사하강법)이라고 한다. 선형회귀에서는 2차함수이므로 극저점이 하나이지만 더 고차함수인 경우 극점이 여러개이므로, 여러 지점에 랜덤지점을 탐색해 그중 최저점을 찾아야 한다.
아래 코드는 weight를 방향에 맞게 조절하며 비용이 최소인 지점을 찾는 코드이다.
import numpy as np
import matplotlib.pyplot as plt
# simple function to demo step size
def f(x): # A parabola
f = 0.5*x**2
return f
def Df(x): # The derivative (gradient)
Df = x*2
return Df
def xp1(x,alpha): # update
xp1 = x - alpha * Df(x)
return xp1
def plot_steps(guess, alpha, nsteps):
fig, ax = plt.subplots()
x = np.linspace(-3,3,100)
ax.plot(x, f(x))
x = guess
ax.plot(x,f(x), ‘o’, label=‘start x=%.2f’ %x )
for i in range(nsteps):
xold = x
x = xp1(x,alpha)
# ax.plot(x,f(x), ‘o’, label=‘x = %.2f’ %x)
ax.plot(x,f(x), ‘o’)
ax.plot([xold,x],[f(xold),f(x)], ‘-‘)
plt.legend()
plt.show()
plot_steps( 3, 0.03, 80 )
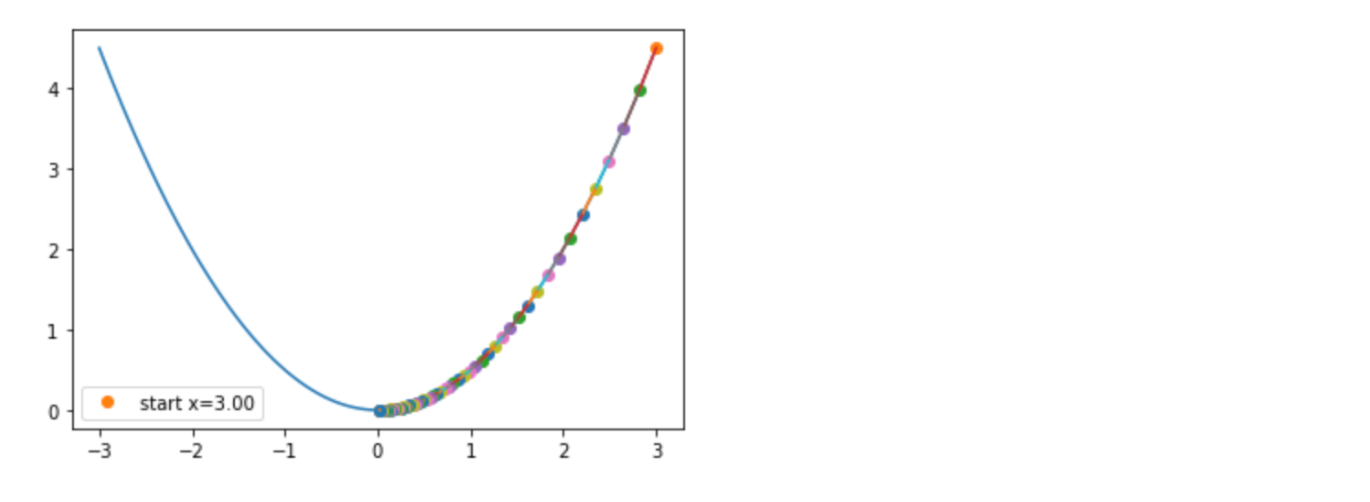
하지만 생각해보면 w와 b는 독립적이기 때문에 2차원으로 표현할 수는 없고 아래처럼 3차원이 될 것이다. 저런 파란 공간에서 노란 구슬이 정답으로 굴러 내려갈 것이다.
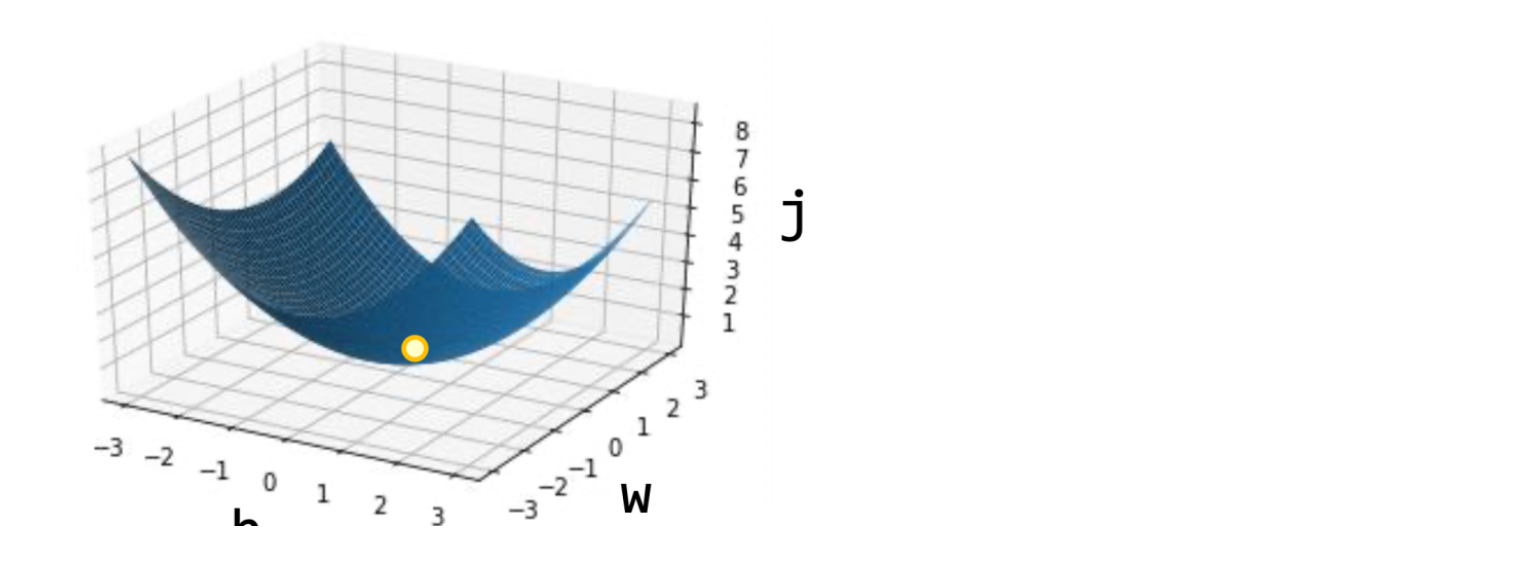
Multi variable Linear Regression
변수가 여러개(Xn)이더라도 방식은 동일하다. 입력은 가중치를 곱하여 다 더해진다. 여러개일때 쉽게 표현하는 방법은 행렬곱이다. GPU가 적합한 이유가 여기에 있다. 이제 이러한 역전파(결과와 정답의 오차를 적용)를 이용하여 실제 선형회귀를 구현해보자. 마지막 스텝이다.
class Neuron:
def __init__(self):
self.w = 1.0 // 가중치를 초기화합니다
self.b = 1.0 // 절편을 초기화합니다
def forpass(self, x):
y_hat = x * self.w + self.b // 직선 방정식을 계산합니다
return y_hat
def backprop(self, x, err):
w_grad = x * err // 가중치에 대한 그래디언트를 계산합니다
b_grad = 1 * err // 절편에 대한 그래디언트를 계산합니다
return w_grad, b_grad
def fit(self, x, y, epochs=100, rate=0.01):
for i in range(epochs): // 에포크만큼 반복합니다
for x_i, y_i in zip(x, y): // 모든 샘플에 대해 반복합니다(zip 활용)
y_hat = self.forpass(x_i) // 정방향 계산
err = y_hat - y_i // 오차 계산
w_grad, b_grad = self.backprop(x_i, err) // 역방향 계산
self.w -= rate*w_grad // 가중치 업데이트
self.b -= rate*b_grad // 절편 업데이트
neuron = Neuron()
neuron.fit(x, y, 1000)
plt.scatter(x, y)
pt1 = (-0.1, -0.1 * neuron.w + neuron.b)
pt2 = (0.15, 0.15 * neuron.w + neuron.b)
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]],’r’)
plt.xlabel(‘x’)
plt.ylabel(‘y’)
plt.show()
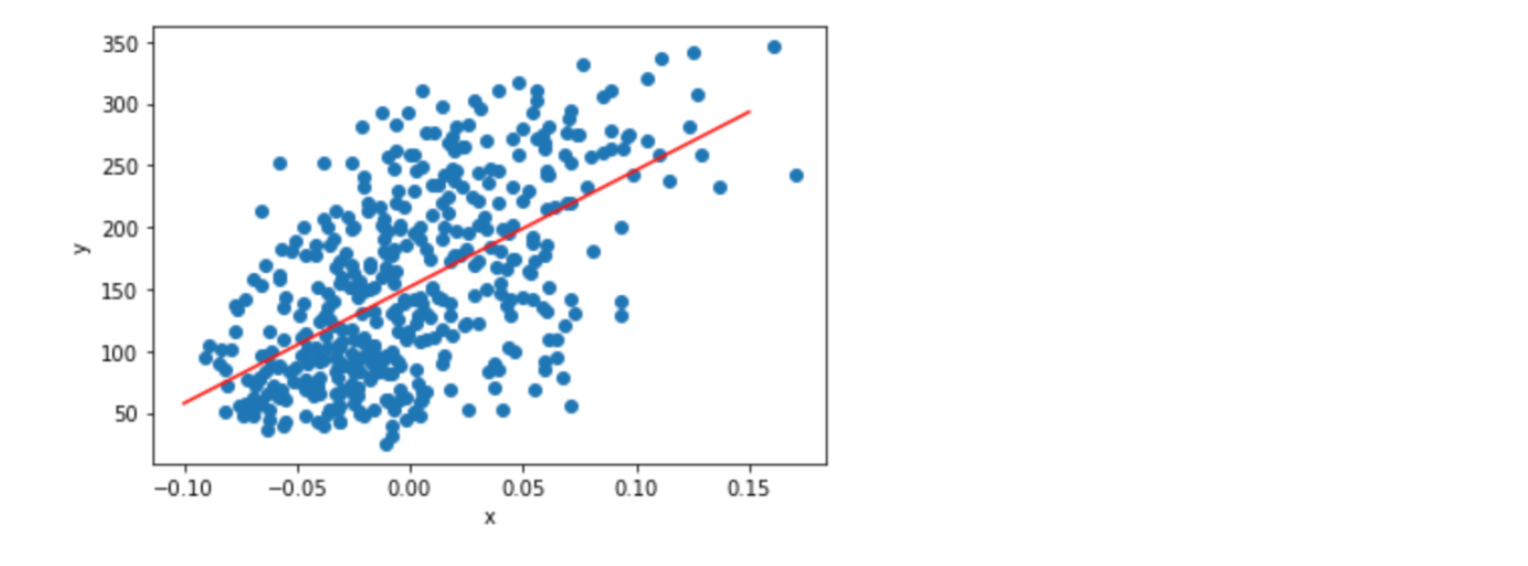
backprop 함수 부분이 중요한데, 이 부분이 역전파 부분이다. 이 과정을 통해 진정으로 학습이 된다고 할 수 있고, 항상 이 계산이 제일 어렵다. (물론 나중에는 tensorflow가 자동으로 미분을 해서 계산해주고, keras를 쓰면 그럴 필요조차도 없다)
def backprop(self, x, err):
w_grad = x * err # 가중치에 대한 그래디언트를 계산
b_grad = 1 * err # 절편에 대한 그래디언트를 계산
return w_grad, b_grad
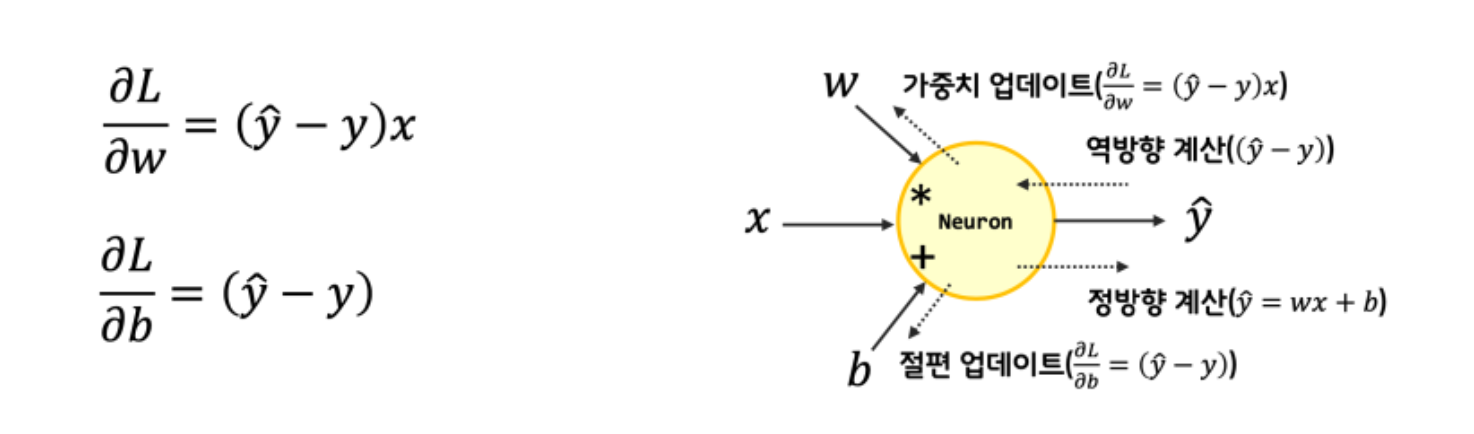
편미분을 해서 weight, bias에 대한 미분값을 구하는 과정이다.
활용
지금까지 한 선형회귀를 어디에 사용할 수 있을까?
데이터를 학습시켜서 weight와 bias를 얻으면(직선을 얻으면), 새로운 입력값이 있을때 어떤 결과를 나타낼지 예측값을 계산할 수 있다!
Linear regression은 예측, Logistic regression은 분류의 목적이라 할 수 있는 것이다.