Multi Layer Perceptron
Perceptron
우선 Perceptron부터 살펴보자. 우리 몸의 신경망은 아래 그림과 같은 모습으로 정보를 전달하는데,
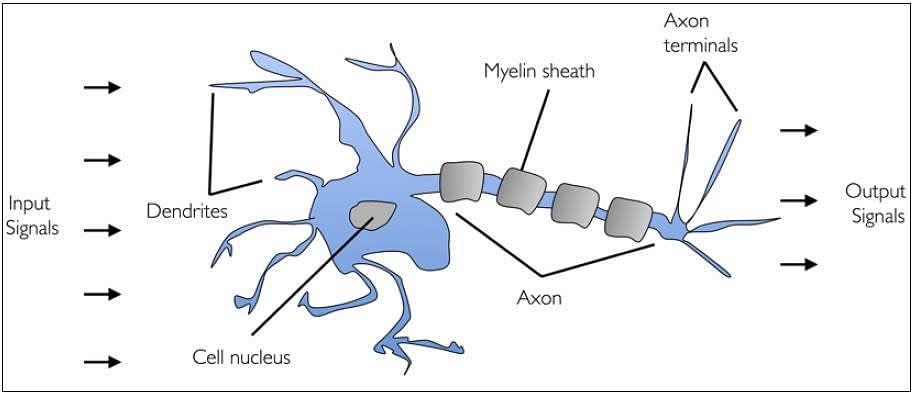
이를 추상화해보면 공학적인 모델이 나오게 된다. 이를 Perceptron이라 한다. 또한 생물학적 신경망을 공학적으로 본떠서 구현하는 방식을 ANN(artificial Neural network)이라고 한다.
추상화된 모델을 정리해보면,
여러 자극 Xn이 뉴런에 전달되면 모이고 역치 이상의 값이 전달되서 다른 뉴런에게 전달된다(output)
S = np.matmul(x, w) +b
라고 할 수 있다.
SLP(Single Layer Perceptrion)
자극 x와 가중치 w의 곱 들의 합이 모이고, b는 기본값(편향)이다.
이렇게 하면 하나의 레이어가 만들어지는 것이다
이 하나의 레이어로 된 Perceptron을 SLP(Single Layer Perceptron)이라 한다.
Disision Boundary
그런데 이런 SLP는 간단한 xor 문제도 해결하지 못한다. 그래서 여러개의 Dicision Boundary의 결과를 AND/OR 등으로 조합해서 특정영역을 선택하는 방식으로 문제를 해결한다. 말하자면 하나의 레이어당 직선 하나를 그릴 수 있는데, 여러 레이어로 여러 직선을 그어서 클래스를 구분하자는 것이다.
Input layer > 각각 Dicision boundary 계산(Hidden layer) > 취합(Output layer)
Tensorflow playground에서 시각적으로 이것을 시각적으로 살펴보자.

직선하나로는 저 부류를 구분하지 못한다. 원 같은 기하 모델을 만들 수도 있지만 수많은 다양한걸 어떻게 수학적으로 계산할것인가? 매번 가설을 세우고 그것에 대한 방정식을 구해서 모델을 만들 것인가?

결과적으로 그려진 점들보고 원인거 같네? 해서 x1^2 + x2^2을 했더니 구분을 하긴 했는데…
강아지 고양이 구분할때도 방정식을 만들것인가? 가능한 일인가?
그래서 직선으로만 한다.
여러개의 뉴런과 레이어로 직선을 조합해서 구분하자.
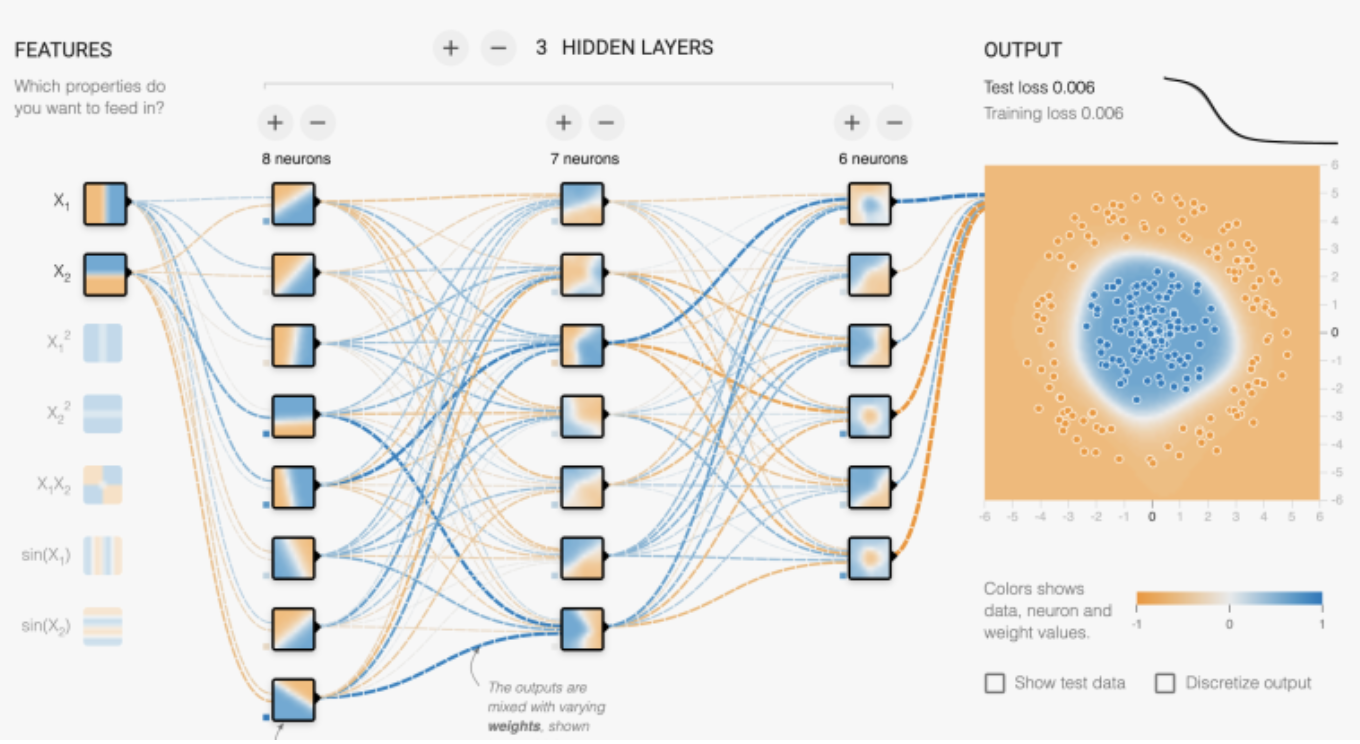
여러 개의 뉴런과 여러 개의 레이어로 직선들을 교차시켜서 구분할수가 있었다. 이 이전까지의 공부는 직선 하나를 긋는 것에 대한 것이었고 이제 다층 레이어를 구성해서 문제를 해결할 수 있게 된 것이다.
그런데 참 신기하게도 여러개의 레이어지만 행렬의 곱을 통해 계산을 하니 멀티레이어지만 계산 방식은 동일하다. 누가 만든건지 잘만들었다 진짜.
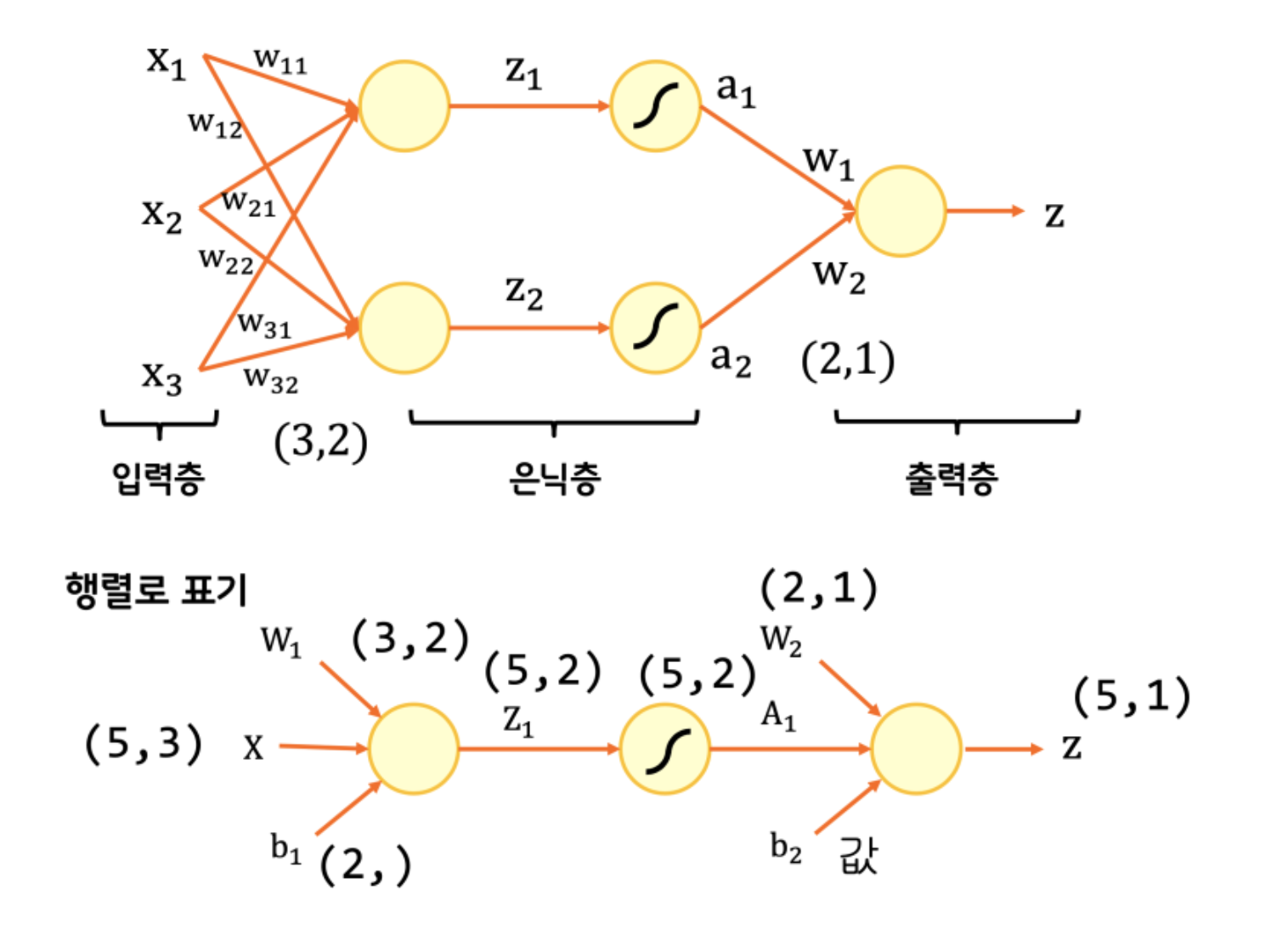
일단 하나의 레이어부터 생각해보면 두 개의 뉴런(노란 동그라미)이 있을때, 각 입력-뉴런에 대해서 가중치가 필요하고 행렬 형태로 표현이 된다. 코드로는 아래와 같다.
class SingleLayer:
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None # 가중치
self.b = None # 절편
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.w_history = [] # 가중치 기록
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
def forpass(self, x):
z = np.dot(x, self.w) + self.b # 선형 출력을 계산합니다.
return z
def backprop(self, x, err):
m = len(x)
w_grad = np.dot(x.T, err) / m # 가중치에 대한 그래디언트를 계산합니다.
b_grad = np.sum(err) / m # 절편에 대한 그래디언트를 계산합니다.
return w_grad, b_grad
def activation(self, z):
z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
a = 1 / (1 + np.exp(-z)) # 시그모이드 계산
return a
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.w = np.ones((x.shape[1], 1)) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = a - y # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w_grad, b_grad = self.backprop(x, err)
# 그래디언트에서 페널티 항의 미분 값을 더합니다.
w_grad += (self.l1 * np.sign(self.w) + self.l2 * self.w) / m
# 가중치와 절편을 업데이트합니다.
self.w -= self.lr * w_grad
self.b -= self.lr * b_grad
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
def predict(self, x):
z = self.forpass(x) # 정방향 계산을 수행합니다.
return z > 0 # 스텝 함수를 적용합니다.
def score(self, x, y):
# 예측과 타깃 열 벡터를 비교하여 True의 비율을 반환합니다.
return np.mean(self.predict(x) == y.reshape(-1, 1))
def reg_loss(self):
# 가중치에 규제를 적용합니다.
return self.l1 * np.sum(np.abs(self.w)) + self.l2 / 2 * np.sum(self.w**2)
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
a = np.clip(a, 1e-10, 1-1e-10) # 출력 값을 클리핑합니다.
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
val_loss = np.sum(-(y_val*np.log(a) + (1-y_val)*np.log(1-a)))
self.val_losses.append((val_loss + self.reg_loss()) / len(y_val))
single layer에 뉴런만 늘어난 코드이기 때문에 기존의 변수 값이 행렬로 바꼈을 뿐 별로 다른점이 없다. 미분은 복잡하지만, 그런건 나중에 텐서플로우가 해주겠지…
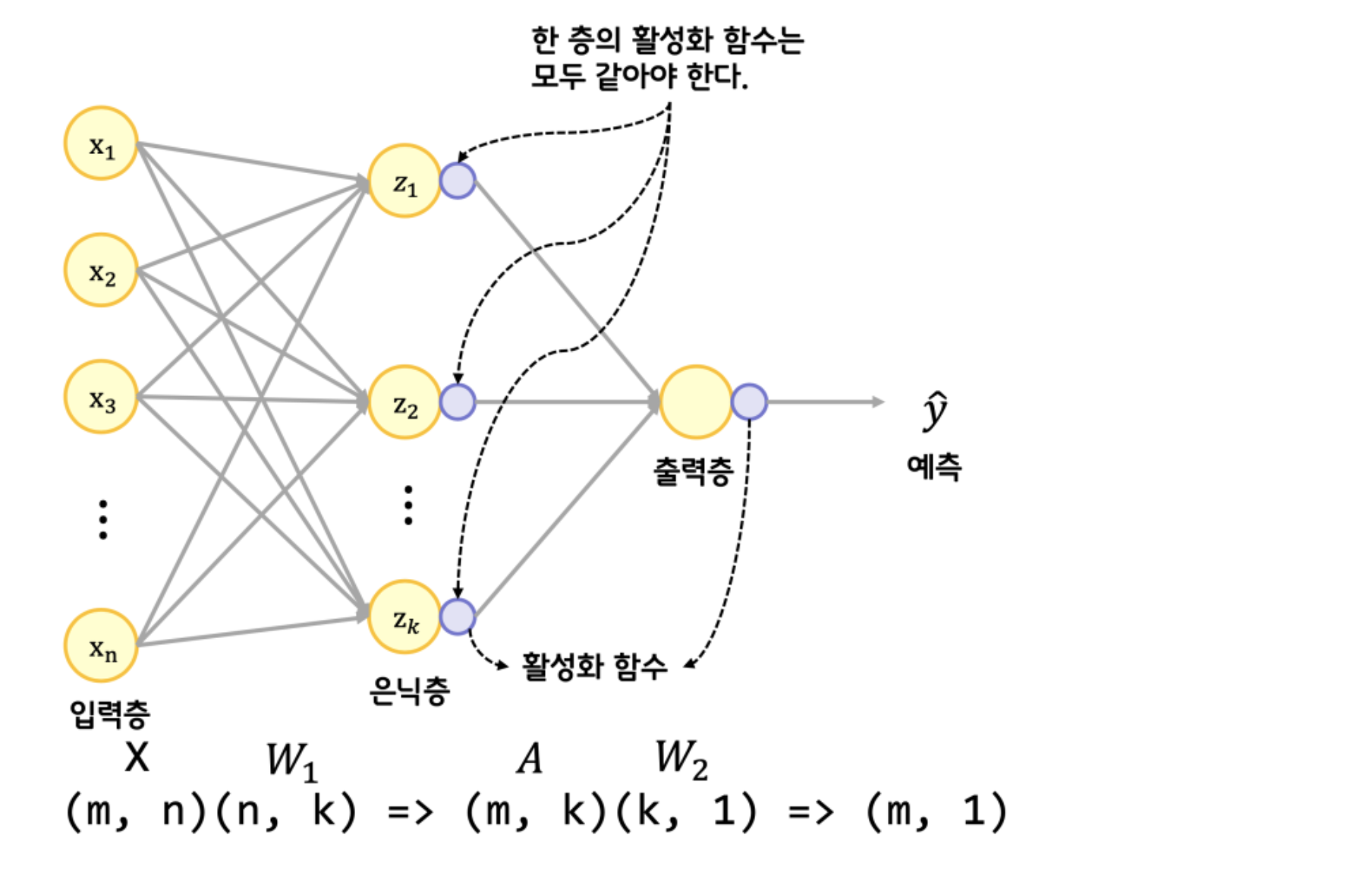
이번엔 Layer까지 두 개인 형태이다. 행렬의 곱으로 표현하니 중간이 쏙 사라지면서 간단해진다. (n과 k가 사라지는 과정)
아래의 영상으로 좀 더 살펴보자.
https://youtu.be/IG85bJh5S8k
여기까지 너무나도 아름다웠다. 누군가 미리 알고 만든 것처럼. 하지만 취합을 위해서는 굉장히 큰 연산이 필요하다. 이 때 이 분야 석학이라는 Minsky 교수가 간단한 MLP에도 값을 찾을 방법이 없다라고 말해서 업계에 큰 겨울이 왔다. Winter is comming이다.
Backpropagation
그런데 시간이 흘러 아래의 방식에 의해서 이 업계에 다시 봄이 왔다.
Backpropagation
취합하는 레이어(Output Layer)부터 역방향으로 기울기를 계산하는 것이다. 이 과정을 통해서 겨우겨우 구한게 y_hat 하나의 값이다. 이걸 또 역전파해서 weight, bias를 조절해야 한다. 한번에 구하려니 엄두가 안난다.
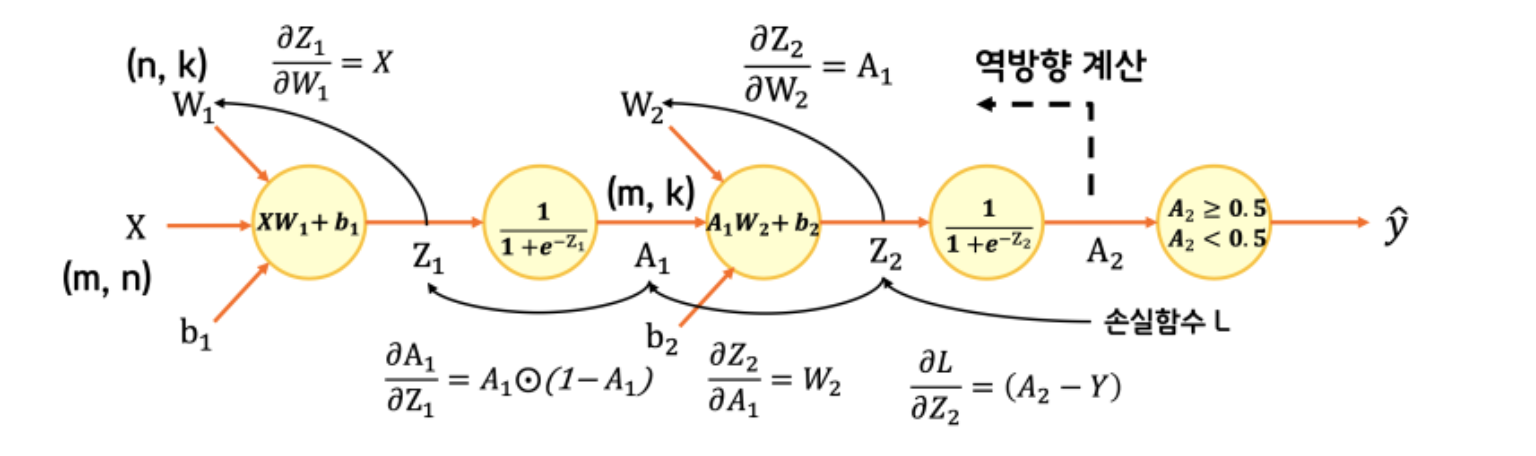
근데 잘생각해보니 체인룰에 따라 아래와 같고,
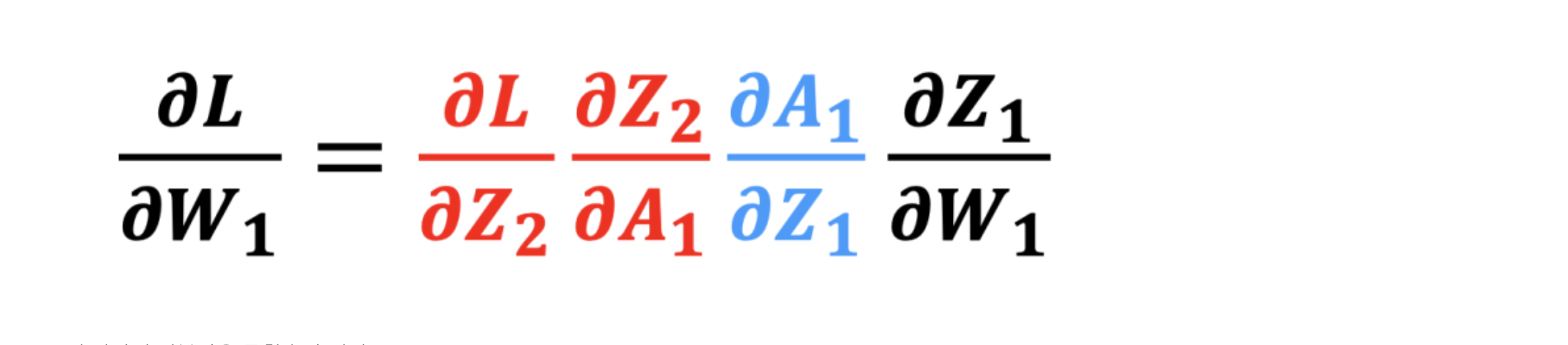
이 각각의 미분값은 구할수가 있다. 각각의 미분값을 구해서 곱하면 최종적으로 w1에 대한 손실의 미분값을 구할 수 있다. 진짜 봄이 온 것이다. 이제 코드로도 아래처럼 구현할 수 있다.
class DualLayer(SingleLayer):
def __init__(self, units=10, learning_rate=0.1, l1=0, l2=0):
self.units = units # 은닉층의 뉴런 개수
self.w1 = None # 은닉층의 가중치
self.b1 = None # 은닉층의 절편
self.w2 = None # 출력층의 가중치
self.b2 = None # 출력층의 절편
self.a1 = None # 은닉층의 활성화 출력
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 # 첫 번째 층의 선형 식을 계산합니다
self.a1 = self.activation(z1) # 활성화 함수를 적용합니다
z2 = np.dot(self.a1, self.w2) + self.b2 # 두 번째 층의 선형 식을 계산합니다.
return z2
def backprop(self, x, err):
m = len(x) # 샘플 개수
# 출력층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w2_grad = np.dot(self.a1.T, err) / m
b2_grad = np.sum(err) / m
# 시그모이드 함수까지 그래디언트를 계산합니다.
err_to_hidden = np.dot(err, self.w2.T) * self.a1 * (1 - self.a1)
# 은닉층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
def init_weights(self, n_features):
self.w1 = np.ones((n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.ones((self.units, 1)) # (은닉층의 크기, 1)
self.b2 = 0
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
y = y.reshape(-1, 1) # 타깃을 열 벡터로 바꿉니다.
y_val = y_val.reshape(-1, 1)
m = len(x) # 샘플 개수를 저장합니다.
self.init_weights(x.shape[1]) # 은닉층과 출력층의 가중치를 초기화합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
a = self.training(x, y, m)
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss = np.sum(-(y*np.log(a) + (1-y)*np.log(1-a)))
self.losses.append((loss + self.reg_loss()) / m)
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
def training(self, x, y, m):
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.activation(z) # 활성화 함수를 적용합니다.
err = -(y - a) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
# 그래디언트에서 페널티 항의 미분 값을 뺍니다
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
# 은닉층의 가중치와 절편을 업데이트합니다.
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
# 출력층의 가중치와 절편을 업데이트합니다.
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
def reg_loss(self):
# 은닉층과 출력층의 가중치에 규제를 적용합니다.
return self.l1 * (np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + \
self.l2 / 2 * (np.sum(self.w1**2) + np.sum(self.w2**2))
single layer 코드와 비교하면결과에 대해 다시 계산을 하는 dual layer 개념이 적용된 것을 알 수 있다. 여기까지의 과정을 쭉 정리하면,
선형회귀부터 시작해서(1차함수),
입력값이 늘어났을때 weight * x의 ‘시그마’를 구했고,
뉴런이 늘어났을때 행렬의 곱을 사용하기 시작했고,
다중레이어에서 결과에 다시 계산을 또하는 형태가 되었다.
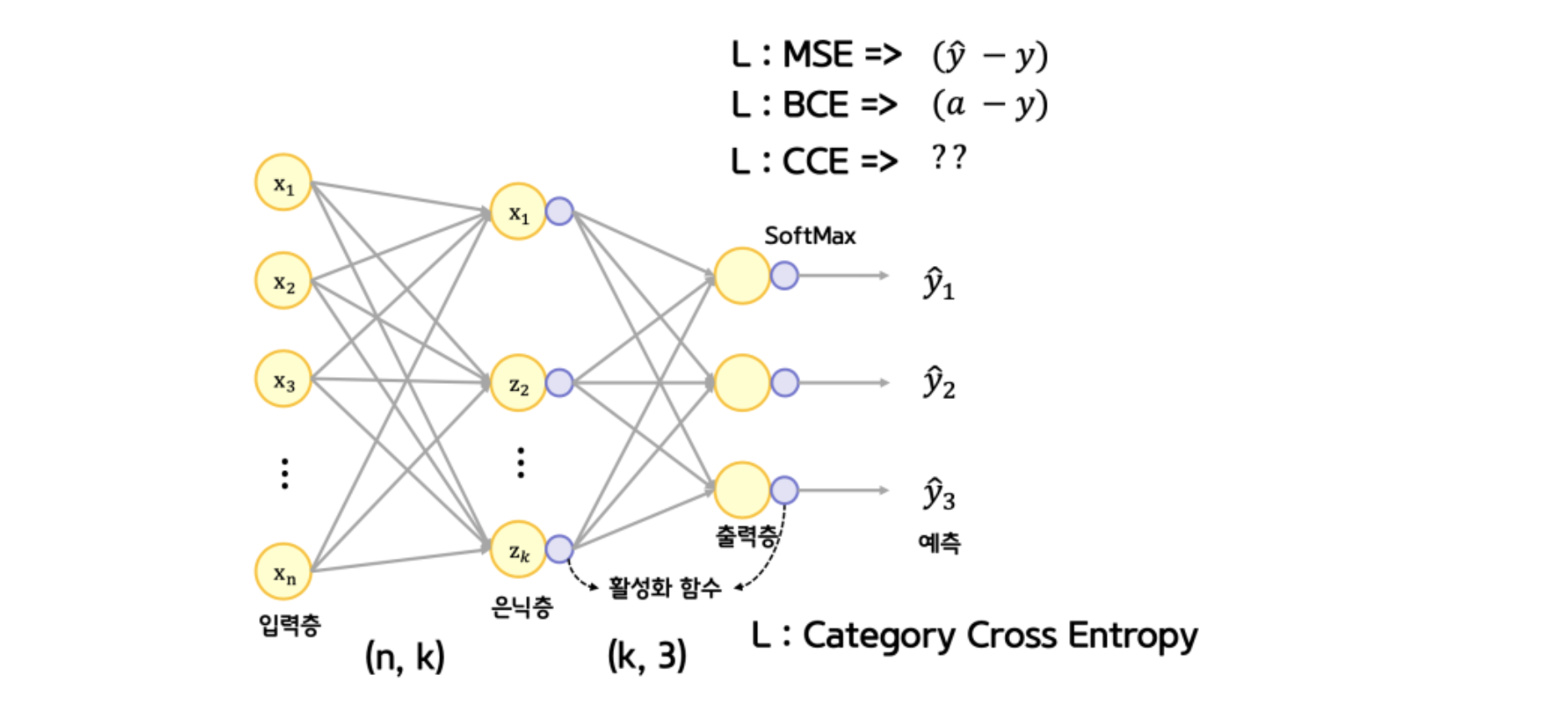
MLP(Multi Layer Perceptron)
이제 한단계 더 가서 출력층이 여러개인 다중분류 신경망이다. 이를 통해 여러 클래스를 구분할 수 있게 된다. (티셔츠, 코트, 반바지, …와 같이 여러개를 분류할 수 있게 되는 것이다)
먼저 아래에서 개념을 잡고 가자.
YouTube
정리하면 분류의 문제를 숫자로 표현하기 위함이다.
YouTube
요약하면 Softmax 함수를 통해 해당 클래스에 해당할 확률을 나타낼 수 있다는 것이다.
오잉 소프트맥스?? 소프트맥스! 창세기전! …
Softmax 함수
소프트맥스 함수를 적용해 출력 강도를 정규화한다.

여러 클래스 중 어느것에 해당하는지를 확률 등으로 나타내기 위해 총합이 1인 형태로 정규화 할 필요가 있고, 이때 소프트맥스 함수를 쓰게된다. 이는 Multinomial Classification이라고도 한다. Logistic Regression을 여러개 이상 진행한다고 볼 수도 있는 것이다.
Category Cross Entropy
비용함수로는 카테고리 크로스 엔트로피(CCE)라는 방식을 사용하게 된다. Dicision boundary 안에 속할지 안속할지의 확률과 가설의 결과를 H(x)라고 할 때, H(x)의 확률 분포를 이용하여 비용을 계산하는 것이다.
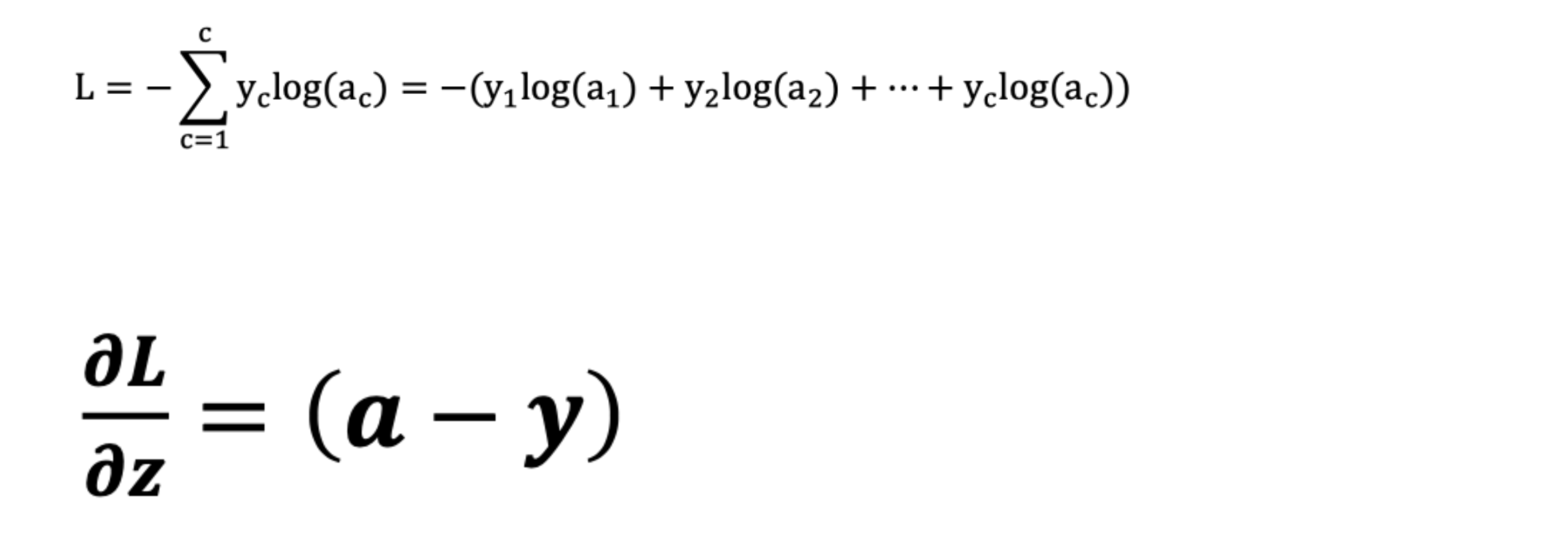
그런데 미분해서 복잡하게 계산하다보면, 결국 확률과 실제 값이 차이가 나온다. 계산에 별로 달라진 것은 없다. 아래의 예로 살펴보면,
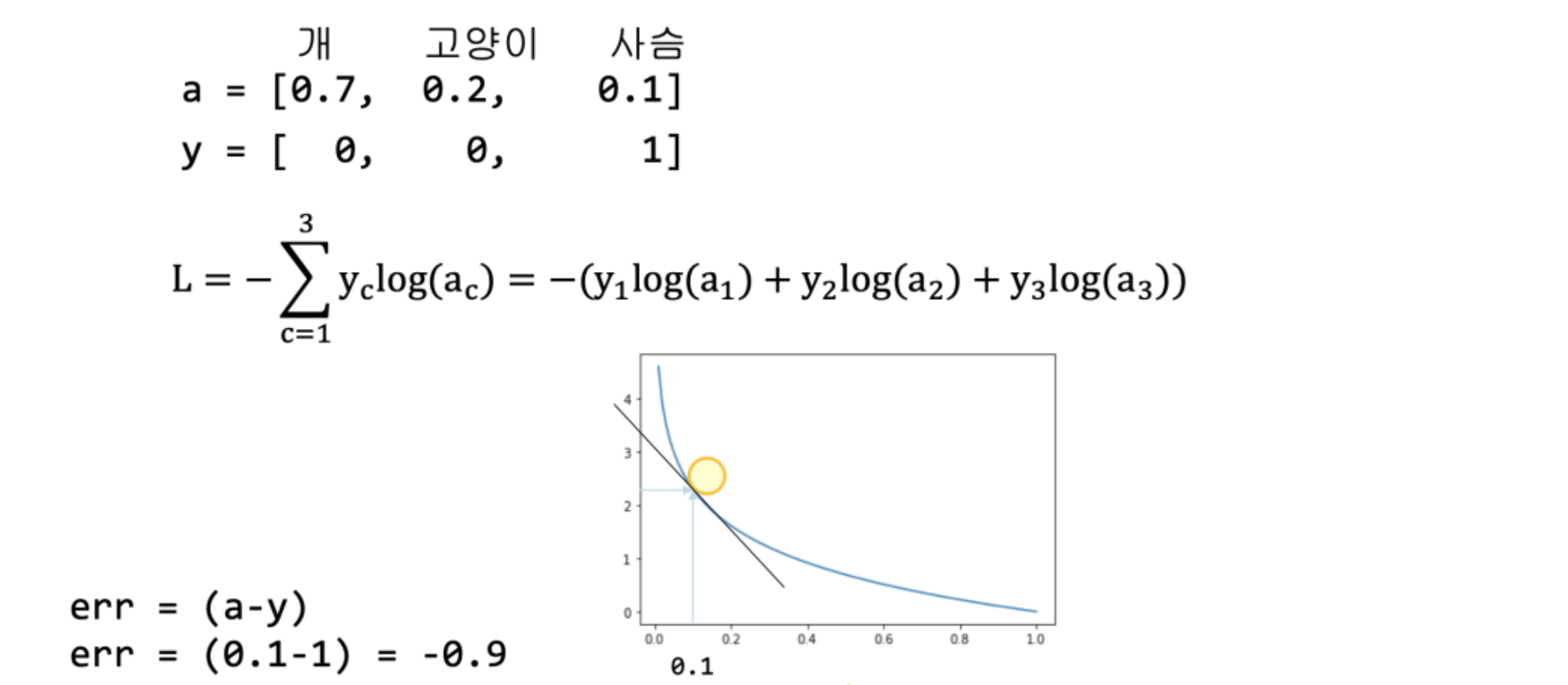
답은 사슴인데 확률이 0.1이다. 많이 틀렸다. 위 비용함수를 보면 y1, y2는 0이기 때문에 결국 세번째 항만 남게되고 쉽게 계산이 가능하다. 역전파해서 weight, bias를 수정한다. 코드로는 아래와 같다.
import numpy as np
class MultiClassNetwork:
def __init__(self, units=10, batch_size=32, learning_rate=0.1, l1=0, l2=0):
self.units = units # 은닉층의 뉴런 개수
self.batch_size = batch_size # 배치 크기
self.w1 = None # 은닉층의 가중치
self.b1 = None # 은닉층의 절편
self.w2 = None # 출력층의 가중치
self.b2 = None # 출력층의 절편
self.a1 = None # 은닉층의 활성화 출력
self.losses = [] # 훈련 손실
self.val_losses = [] # 검증 손실
self.lr = learning_rate # 학습률
self.l1 = l1 # L1 손실 하이퍼파라미터
self.l2 = l2 # L2 손실 하이퍼파라미터
def forpass(self, x):
z1 = np.dot(x, self.w1) + self.b1 # 첫 번째 층의 선형 식을 계산합니다
self.a1 = self.sigmoid(z1) # 활성화 함수를 적용합니다
z2 = np.dot(self.a1, self.w2) + self.b2 # 두 번째 층의 선형 식을 계산합니다.
return z2
def backprop(self, x, err):
m = len(x) # 샘플 개수
# 출력층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w2_grad = np.dot(self.a1.T, err) / m
b2_grad = np.sum(err) / m
# 시그모이드 함수까지 그래디언트를 계산합니다.
err_to_hidden = np.dot(err, self.w2.T) * self.a1 * (1 - self.a1)
# 은닉층의 가중치와 절편에 대한 그래디언트를 계산합니다.
w1_grad = np.dot(x.T, err_to_hidden) / m
b1_grad = np.sum(err_to_hidden, axis=0) / m
return w1_grad, b1_grad, w2_grad, b2_grad
def sigmoid(self, z):
z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
a = 1 / (1 + np.exp(-z)) # 시그모이드 계산
return a
def softmax(self, z):
# 소프트맥스 함수
z = np.clip(z, -100, None) # 안전한 np.exp() 계산을 위해
exp_z = np.exp(z)
return exp_z / np.sum(exp_z, axis=1).reshape(-1, 1)
def init_weights(self, n_features, n_classes):
self.w1 = np.random.normal(0, 1,
(n_features, self.units)) # (특성 개수, 은닉층의 크기)
self.b1 = np.zeros(self.units) # 은닉층의 크기
self.w2 = np.random.normal(0, 1,
(self.units, n_classes)) # (은닉층의 크기, 클래스 개수)
self.b2 = np.zeros(n_classes)
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
np.random.seed(42)
self.init_weights(x.shape[1], y.shape[1]) # 은닉층과 출력층의 가중치를 초기화합니다.
# epochs만큼 반복합니다.
for i in range(epochs):
loss = 0
print(‘.’, end=‘’)
# 제너레이터 함수에서 반환한 미니배치를 순환합니다.
for x_batch, y_batch in self.gen_batch(x, y):
a = self.training(x_batch, y_batch)
# 안전한 로그 계산을 위해 클리핑합니다.
a = np.clip(a, 1e-10, 1-1e-10)
# 로그 손실과 규제 손실을 더하여 리스트에 추가합니다.
loss += np.sum(-y_batch*np.log(a))
self.losses.append((loss + self.reg_loss()) / len(x))
# 검증 세트에 대한 손실을 계산합니다.
self.update_val_loss(x_val, y_val)
# 미니배치 제너레이터 함수
def gen_batch(self, x, y):
length = len(x)
bins = length // self.batch_size # 미니배치 횟수
if length % self.batch_size:
bins += 1 # 나누어 떨어지지 않을 때
indexes = np.random.permutation(np.arange(len(x))) # 인덱스를 섞습니다.
x = x[indexes]
y = y[indexes]
for i in range(bins):
start = self.batch_size * i
end = self.batch_size * (i + 1)
yield x[start:end], y[start:end] # batch_size만큼 슬라이싱하여 반환합니다.
def training(self, x, y):
m = len(x) # 샘플 개수를 저장합니다.
z = self.forpass(x) # 정방향 계산을 수행합니다.
a = self.softmax(z) # 활성화 함수를 적용합니다.
err = (a - y) # 오차를 계산합니다.
# 오차를 역전파하여 그래디언트를 계산합니다.
w1_grad, b1_grad, w2_grad, b2_grad = self.backprop(x, err)
# 그래디언트에서 페널티 항의 미분 값을 뺍니다
w1_grad += (self.l1 * np.sign(self.w1) + self.l2 * self.w1) / m
w2_grad += (self.l1 * np.sign(self.w2) + self.l2 * self.w2) / m
# 은닉층의 가중치와 절편을 업데이트합니다.
self.w1 -= self.lr * w1_grad
self.b1 -= self.lr * b1_grad
# 출력층의 가중치와 절편을 업데이트합니다.
self.w2 -= self.lr * w2_grad
self.b2 -= self.lr * b2_grad
return a
def predict(self, x):
z = self.forpass(x) # 정방향 계산을 수행합니다.
return np.argmax(z, axis=1) # 가장 큰 값의 인덱스를 반환합니다.
def score(self, x, y):
# 예측과 타깃 열 벡터를 비교하여 True의 비율을 반환합니다.
return np.mean(self.predict(x) == np.argmax(y, axis=1))
def reg_loss(self):
# 은닉층과 출력층의 가중치에 규제를 적용합니다.
return self.l1 * (np.sum(np.abs(self.w1)) + np.sum(np.abs(self.w2))) + \
self.l2 / 2 * (np.sum(self.w1**2) + np.sum(self.w2**2))
def update_val_loss(self, x_val, y_val):
z = self.forpass(x_val) # 정방향 계산을 수행합니다.
a = self.softmax(z) # 활성화 함수를 적용합니다.
a = np.clip(a, 1e-10, 1-1e-10) # 출력 값을 클리핑합니다.
# 크로스
코드가 더 길어졌다. 그런데…
rom tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
model = Sequential()
model.add(Dense(100, activation=‘sigmoid’, input_shape=(784,)))
model.add(Dense(10, activation=‘softmax’))
model.compile(optimizer=‘sgd’, loss=‘categorical_crossentropy’,
metrics=[‘accuracy’])
history = model.fit(x_train, y_train_encoded, epochs=40,
validation_data=(x_val, y_val_encoded))
Keras로 해보니 많이 추상화 되어있어서 참 쉽다.